阿里巴巴笔试题选解
--9月22日,阿里巴巴北邮站
小题:(部分题目)
1、有三个结点的,可以构成多少个种叉树?
2、一副牌52张(去掉大小王),从中抽取两张牌,一红一黑的概率是多少?
编程题:
3、设计一个最优算法来查找一n个元素数组中的最大值和最小值。已知一种需要比较2n次的方法,请给一个更优的算法。情特别注意优化时间复杂度的常数。
4、已知三个升序整数数组a[l], b[m]和c[n]。请在三个数组中各找一个元素,是的组成的三元组距离最小。三元组的距离定义是:假设a[i]、b[j]和c[k]是一个三元组,那么距离为:
Distance = max(|a[ I ] – b[ j ]|, |a[ I ] – c[ k ]|, |b[ j ] – c[ k ]|)
请设计一个求最小三元组距离的最优算法,并分析时间复杂度。
5、在黑板上写下50个数字:1至50.在接下来的49轮操作中,每次做如下动作:选取两个黑板上的数字a和b,擦去,在黑板上写|b - a|。请问最后一次动作之后剩下数字可能是什么?为什么?
题解:(题解非官方,仅供参考,有错误的地方望指正!谢谢)
1、有三个结点的,可以构成多少个种树形结构?
解:应该是5种;

2、一副牌52张(去掉大小王),从中抽取两张牌,一红一黑的概率是多少?
考察概率论知识
解法一: 52张牌从中抽两张,就是 C(2,52)种情况,一红一黑是C(1,26) * C(1,26)种
P = [C(1,26) * C(1,26) ] / C(2,52) = 26 * 26 / (26 * 51) = 26/51
解法二: 全为黑或者全为红是C(2,26)种情况,由于是黑和红两种,所以要乘以2
P = 1 - C(2,26) / C(2,52) - C(2,26) / C(2,52) = 1 - 2 * (26 * 25)/(51 * 52) = 1 - 25/51 = 26/51
3、设计一个最优算法来查找一n个元素数组中的最大值和最小值。已知一种需要比较2n次的方法,请给一个更优的算法。情特别注意优化时间复杂度的常数。
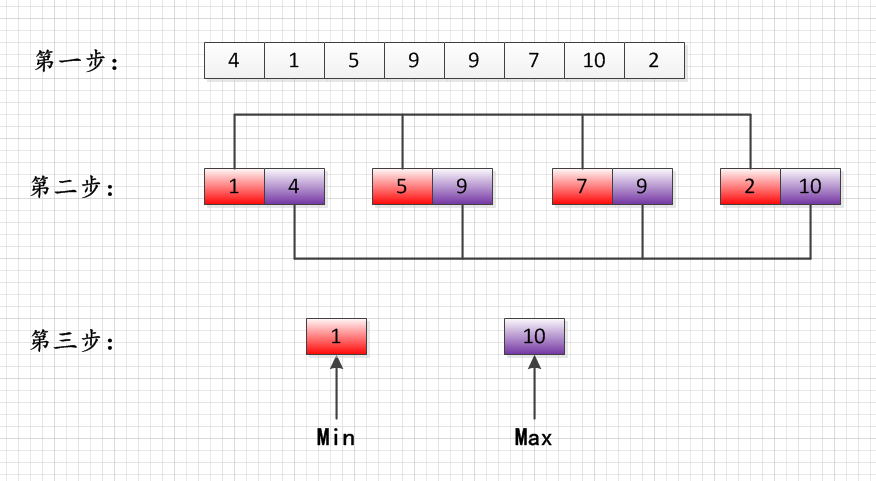
解:把数组两两一对分组,如果数组元素个数为奇数,就最后单独分一个,然后分别对每一组的两个数比较,把小的放在左边,大的放在右边,这样遍历下来,总共比较的次数是 N/2 次;在前面分组的基础上,那么可以得到结论,最小值一定在每一组的左边部分找,最大值一定在数组的右边部分找,最大值和最小值的查找分别需要比较N/2 次和N/2 次;这样就可以找到最大值和最小值了,比较的次数为
N/2 * 3 = (3N)/2 次
如图会更加清晰:
代码实现:


#include#include #define N 8int main(void){ //int arr[N] = {4, 1, 5, 9, 9, 7, 10}; int arr[N] = { 1,2,3,4,5,6,9,1}; int iter = 0; int cnt = 0; for(iter = 0; iter < N ; iter += 2) { if(++cnt && arr[iter] > arr[iter + 1] ) { int temp = arr[iter]; arr[iter] = arr[iter + 1]; arr[iter + 1] = temp; } } int i = 0; for(i = 0; i < N; i++) { printf("%-3d", arr[i]); } printf("\n"); int myMin = arr[0]; for(iter = 2; iter < N ; iter += 2) { if(++cnt && arr[iter] < myMin) { myMin = arr[iter]; } } int myMax = arr[1]; for(iter = 3; iter < N; iter += 2) { if(++cnt && arr[iter] > myMax) { myMax = arr[iter]; } } if(N % 2 != 0 && ++cnt && myMax < arr[N - 1]) myMax = arr[N - 1]; printf("min is %d\n", myMin); printf("max is %d\n", myMax); printf("compare times is %d", cnt); return 0;}
上面的算法比较次数基本上已经是最优了,但是有朋友提出这样的顾虑,在极端的情况下,每次都做交换,可能会导致程序开销很大,这样的顾虑是对的,其实在上面的算法的基础上,可以不做交换就能找到最大值和最小值。
第3题 改进的算法:
依旧把数组两两一组分配,不做交换操作,设置一个最大值Max和最小值Min,依次和每一组的两个数据做比较,把较大的值给Max,较小的值给Min,遍历一次就能找到数组的最大值和最小值。
示例:数组为{(4, 1) , (5, 9) , (9 ,7) ,(10,2)},经过第一组比较得到Max = 4,Min = 1,其中比较了3次;,经过第二组比较得到Max = 9,Min = 1,其中比较了3次;……到最后Max = 10,Min = 1;比较次数是3 * N/2 = (3N)/2,比较次数没有改变!代码实现不难,就不贴了
4、已知三个升序整数数组a[l], b[m]和c[n]。请在三个数组中各找一个元素,是的组成的三元组距离最小。三元组的距离定义是:假设a[i]、b[j]和c[k]是一个三元组,那么距离为:
Distance = max(|a[ I ] – b[ j ]|, |a[ I ] – c[ k ]|, |b[ j ] – c[ k ]|)
请设计一个求最小三元组距离的最优算法,并分析时间复杂度。
解:这道题目有两个关键点:
第一个关键点: max{|x1-x2|,|y1-y2|} =(|x1+y1-x2-y2|+|x1-y1-(x2-y2)|)/2 --公式(1)
我们假设x1=a[ i ],x2=b[ j ],x3=c[ k ],则
Distance = max(|x1 – x2|, |x1 – x3|, |x2 – x3|) = max( max(|x1 – x2|, |x1 – x3|) , |x2 – x3|) --公式(2)
根据公式(1),max(|x1 – x2|, |x1 – x3|) = 1/2 ( |2x1 – x2– x3| + |x2 – x3|),带入公式(2),得到
Distance = max( 1/2 ( |2x1 – x2– x3| + |x2 – x3|) , |x2 – x3| )
=1/2 * max( |2x1 – x2– x3| , |x2 – x3| ) + 1/2*|x2 – x3| //把相同部分1/2*|x2 – x3|分离出来
=1/2 * max( |2x1 – (x2 + x3)| , |x2 – x3| ) + 1/2*|x2 – x3| //把(x2 + x3)看成一个整体,使用公式(1)
=1/2 * 1/2 *((|2x1 – 2x2| + |2x1 – 2x3|) + 1/2*|x2 – x3|
=1/2 *|x1 – x2| + 1/2 * |x1 – x3| + 1/2*|x2 – x3|
=1/2 *(|x1 – x2| + |x1 – x3| + |x2 – x3|) //求出来了等价公式,完毕!
第二个关键点:如何找到(|x1 – x2| + |x1 – x3| + |x2 – x3|) 的最小值,x1,x2,x3,分别是三个数组中的任意一个数,这一题,我只是做到了上面的推导,后面的算法设计是由csdn上的两个朋友想出来的方法,他们的CSDN的ID分别为 “云梦泽” 和 “shuyechengying ”.
算法思想是:
用三个指针分别指向a,b,c中最小的数,计算一次他们最大距离的Distance ,然后在移动三个数中较小的数组指针,再计算一次,每次移动一个,直到其中一个数组结束为止,最慢(l+ m + n)次,复杂度为O(l+ m + n)
代码如下:


#include#include #include #define l 3#define m 4#define n 6int Mymin(int a, int b, int c){ int Min = a < b ? a : b; Min = Min < c ? Min : c; return Min;}int Solvingviolence(int a[], int b[], int c[]){ //暴力解法,大家都会,不用过多介绍了! int i = 0, j = 0, k = 0; int MinSum = (abs(a[i] - b[j]) + abs(a[i] - c[k]) + abs(b[j] - c[k])) / 2;// int store[3] = {0}; int Sum = 0; for(i = 0; i < l; i++) { for(j = 0; j < m; j++) { for(k = 0; k < n; k++) { Sum = (abs(a[i] - b[j]) + abs(a[i] - c[k]) + abs(b[j] - c[k])) / 2; if(MinSum > Sum) { MinSum = Sum;// store[0] = i;// store[1] = j;// store[2] = k; } } } }// printf("the min is %d\n", minABC);// printf("the three number is %-3d%-3d%-3d\n", a[store[0]], b[store[1]], c[store[2]]); return MinSum;}int MinDistance(int a[], int b[], int c[]){ int MinSum = 0; //最小的绝对值和 int Sum = 0; //计算三个绝对值的和,与最小值做比较 int MinOFabc = 0; // a[i] , b[j] ,c[k]的最小值 int cnt = 0; //循环次数统计,最多是l + m + n次 int i = 0, j = 0, k = 0; //a,b,c三个数组的下标索引 MinSum = (abs(a[i] - b[j]) + abs(a[i] - c[k]) + abs(b[j] - c[k])) / 2; for(cnt = 0; cnt <= l + m + n; cnt++) { Sum = (abs(a[i] - b[j]) + abs(a[i] - c[k]) + abs(b[j] - c[k])) / 2; MinSum = MinSum < Sum ? MinSum : Sum; MinOFabc = Mymin(a[i] ,b[j] ,c[k]);//找到a[i] ,b[j] ,c[k]的最小值 //判断哪个是最小值,做相应的索引移动 if(MinOFabc == a[i]) { if(++i >= l) break; }//a[i]最小,移动i if(MinOFabc == b[j]) { if(++j >= m) break; }//b[j]最小,移动j if(MinOFabc == c[k]) { if(++k >= n) break; }//c[k]最小,移动k } return MinSum;}int main(void){ int a[l] = { 5, 6, 7}; int b[m] = { 13, 14, 15, 17}; int c[n] = { 19, 22, 24, 29, 32, 42}; printf("\nBy violent solution ,the min is %d\n", Solvingviolence(a, b, c)); printf("\nBy Optimal solution ,the min is %d\n", MinDistance(a, b, c)); return 0;}
5、这几天有点事,第5题还没仔细研究,要是解出来会第一时间更新博客!有求解方法的朋友欢迎评论!
题目部分摘取自july CSDN网站: